세 점 A( -2. 2). B(4. -2), C(4. a)를꼭잣점으로하 는 삼각형 ABC의 넓이가 21일 때, 양수 a의 값을 구하

-2), C(4. a)를 꼭짓점으로
1 는 삼각형 ABC의 넓이가 21일 때, 양수a의 값을구쵸
시오.
삼각형의 넓이가 가이라는 것은
1
- 밑변 x높이 이므로
2
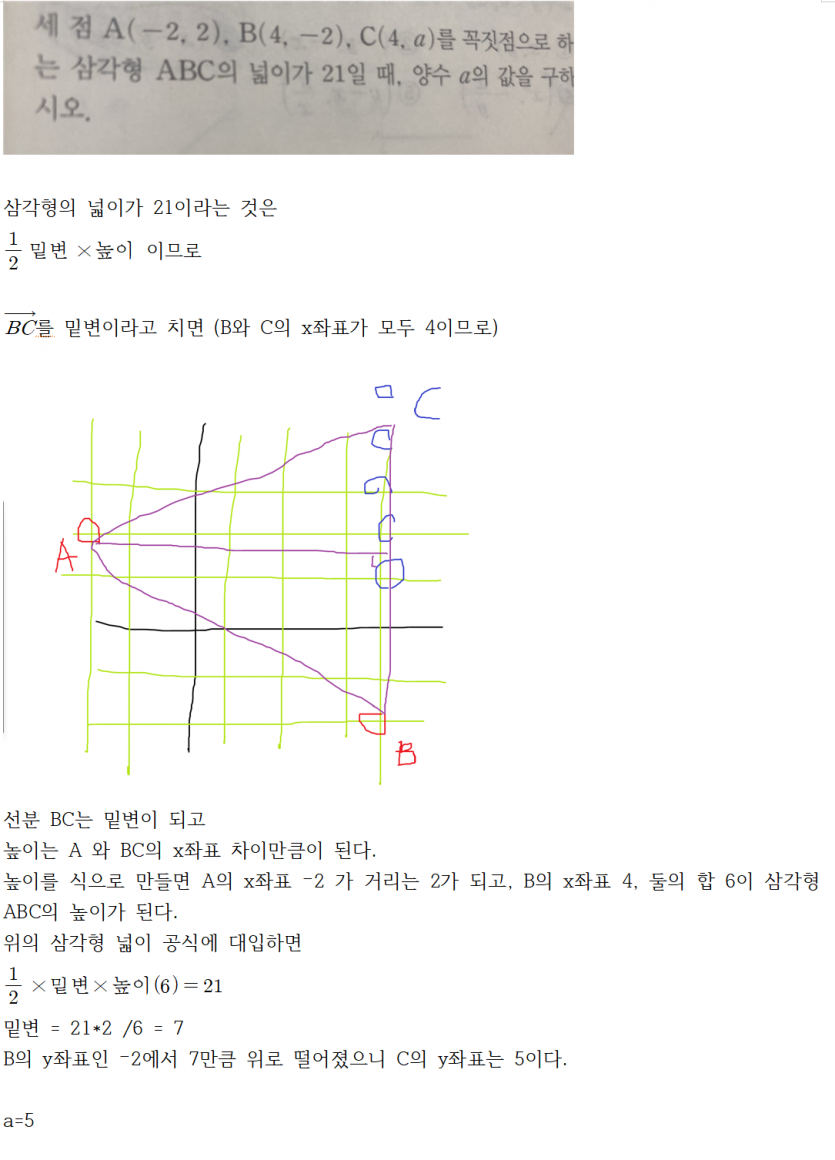
BC를 밑변이라고 치면 (B와 c의 Ⅹ좌표가 모두 4이므로)
선분 BC는 밑변이 되고
높이는 A 와 BC의 )(좌표 차이만큼이 된다.
높이를 식으로 만들면 A의 )(좌표 -2 가 거리는 2가 되고, B의 )(좌표 4, 둘의 합 6이 삼각형
ABC의 높이가 된다.
위의 삼각형 넓이 공식에 대입하면
1
x밑변x높이 (6)=21
2
밑변 = 21*2 /6 = 7
B의 y좌표인 -2에서 7만큼 위로 떨어졌으니 c의 y좌표는 5이다.
a=5

0966 @
점 (6, -2)와y축에 대하여 대칭인 점의 좌표가 (a, b)이
고 원점에 대하여 대칭인 점의 좌표가 (c, d)일 때,
a十b十c十d의 값을 구하시오.
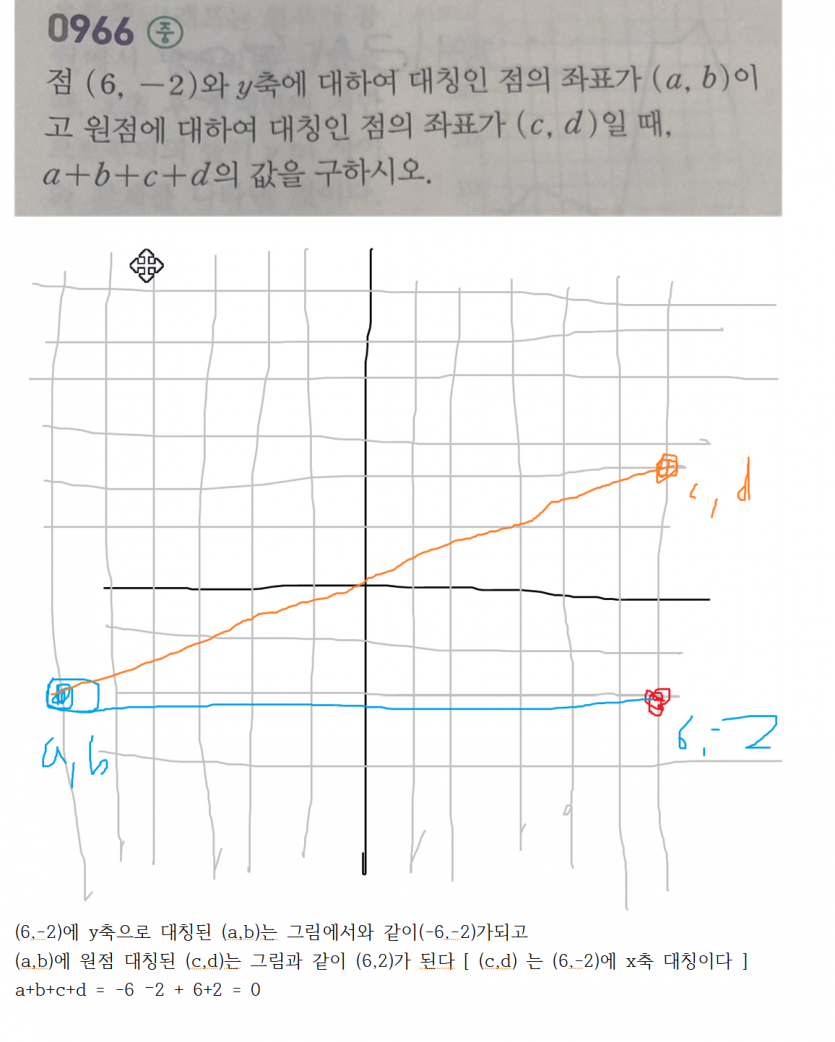
(이-기에 y축으로 대칭된 (하비는 그림에서와 같이(-6,-2)가되고
(하비에 원점 대칭된 (c,d)는 그림과 같이 (이기가 된다 [ (c,d) 는 (이-기에 )(축 대칭이다 ]
a+b+c+d = -6 -2 + 6+2 = 0

0967 ㉯ ~
점 A(2, -4)와 瑟축에 대하여 대칭인 점을 B, 원점에 대
하여 대칭인 점을 C라 할 때, 삼각형 ABC의 넓이를 구하
시오.
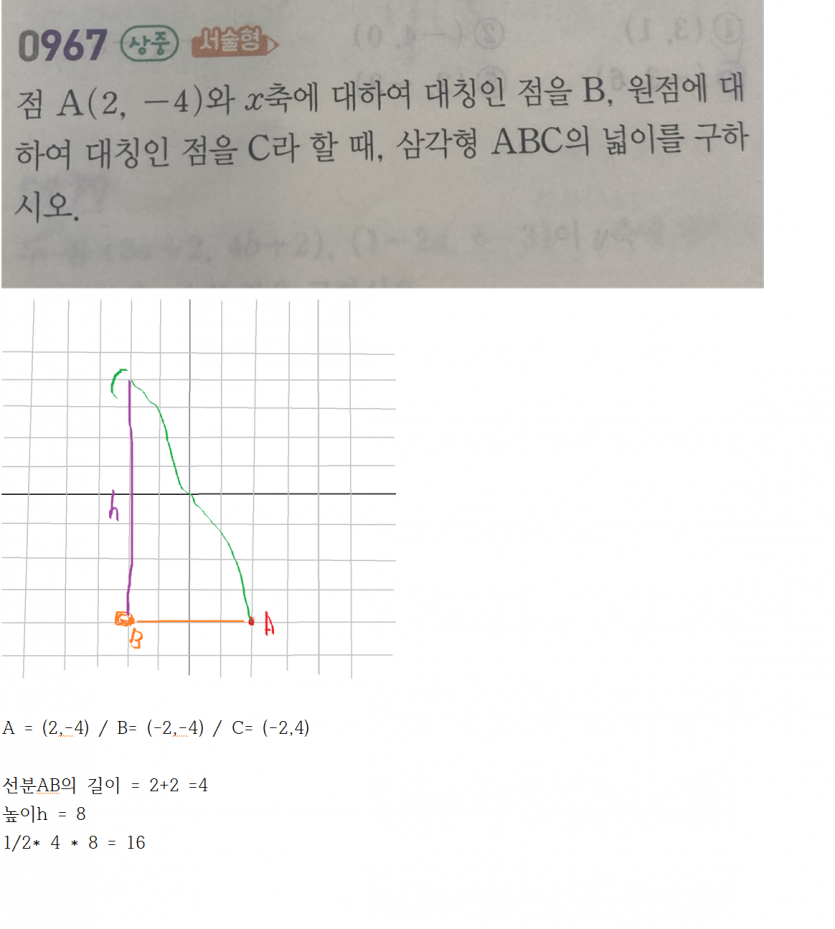
년분AB의 길이
= 2+2 =4
듶이h = 8
/2* 4 * 8= 16